Existencia de soluciones débiles para una clase de sistemas elípticos semilineales
DOI:
https://doi.org/10.15381/pes.v21i1.15078Palabras clave:
ecuación elíptica degenerada, sistema elíptico semilineal, teorema del paso de la montañaResumen
Este artículo resume las contribuciones principales de la tesis con el título “Existencia de soluciones para una clase de sistemas elípticos semilineales". Esta tesis se centra en una exposición didáctica del artículo publicado por Afrouzi, G., Mirzapour, A. and Zographopoulos, N. [1], cuyo objetivo es probar la existencia de soluciones débiles para una clase de sistemas elípticos semilineales potenciales de la forma.
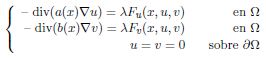
donde el dominio Ω es un dominio acotado en ℝN (N > 2), de frontera bien regular, los pesos a(x), b(x) son pesos medibles no negativas sobre Ω, (Fu, Fv) = ∇F representa el gradiente de F en las variables (u; v) ∈ ℝ2 y λ es un parámetro positivo.
Descargas
Publicado
Número
Sección
Licencia
Derechos de autor 2018 Marlon Yvan Tineo Condeña

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
LOS AUTORES RETIENEN SUS DERECHOS:
a) Los autores retienen sus derechos de marca y patente, y tambien sobre cualquier proceso o procedimiento descrito en el artículo.
b) Los autores retienen el derecho de compartir, copiar, distribuir, ejecutar y comunicar públicamente el artículo publicado en la revista Pesquimat (por ejemplo, colocarlo en un repositorio institucional o publicarlo en un libro), con un reconocimiento de su publicación inicial en la revista Pesquimat.
c) Los autores retienen el derecho a hacer una posterior publicación de su trabajo, de utilizar el artículo o cualquier parte de aquel (por ejemplo: una compilación de sus trabajos, notas para conferencias, tesis, o para un libro), siempre que indiquen la fuente de publicación (autores del trabajo, revista, volumen, numero y fecha).













