ARTÍCULOS PRIMARIOS
Un modelo para el estudio del crecimiento del área corporal en bovinos de carne
A model for the study of the growth of body area in beef cattle
Pere Miquel Parés-Casanova1,2
1. Departament de Ciència Animal, Universitat de Lleida, Catalunya, España
2. E-mail: peremiquelp@ca.udl.cat
RESUMEN
Para el establecimiento del área corporal (Body Surface Area, BSA) se han establecido fórmulas de estimación que parten de peso vivo (PV) y longitud corporal para su cálculo. El objetivo de este trabajo fue comparar cuatro fórmulas de estimación de la BSA – Mitchell [0.09 × PV0.69], Brody [0.14 × PV0.57], Johnson et al. [0.235 × PV0.49], Moulton [0.158 × PV5/8] y Hogan y Skouby [PV0.4 × (longitud corporal)0.6 × 217] – y tres modelos no lineales – logístico [y=a/(1+be-cx)], Gompertz [y=a*exp(b*exp(cx))] y von Bertalanffy [y=a(1-be-cx)] – en cuanto a su capacidad para describir el crecimiento de la BSA en bovinos de carne y detectar la mejor estimación. Se trabajó con una muestra de 53 bovinos de aptitud cárnica (20 machos y 33 hembras), mayormente Bruna de los Pirineos y sus cruces, con edades entre 205 y 407 días, peso vivo estimado de 543±74 kg, sacrificados en un matadero frigorífico. Luego del desollado, se obtuvo una fotografía del cuero extendido y por métodos digitales se obtuvo la BSA. La BSA fue de 3.79±1.37 m2 (rango 2.55-8.12 m2). La fórmula de Hogan y Skouby parecería la más ajustada de las cuatro estimaciones consideradas, con un nivel de determinación de más del 58%, siendo la diferencia en los valores debido probablemente a que la superficie de la cabeza y de las partes distales de las extremidades no fueron consideradas en el trabajo, al quedar separadas en el proceso del desollado. Entre los modelos no lineales, el de mejor ajuste fue el logístico, aunque con un nivel de determinación mucho más bajo, entorno de 2%. De los datos se desprende que el área corporal no ha llegado aún a su desarrollo definitivo a los 400 días de edad en este tipo de animales, lo cual debería tenerse en cuenta al establecer curvas de desarrollo corporal y nuevas fórmulas estimativas más ajustadas.
Palabras clave: alometría; modelo logístico; modelo von Bertalanffy; modelo Gompertz; ontogenia
ABSTRACT
Estimation formulas have been established for the establishment of body surface area (BSA), using live weight (LW) and body length for calculation. The objective of this work was to compare four estimation formulas of the BSA – Mitchell [0.09 × LW0.69], Brody [0.14 × LW0.57], Johnson et al. [0.235 × LW0.49], Moulton [0.158 × LW5/8] and Hogan and Skouby [LW0.4 × (body length)0.6 × 217] – and three non-linear models – logistic [– y=a/(1 + be-cx)], Gompertz [y=a*exp(b*exp(cx))] and von Bertalanffy [y=a(1-be-cx)] – in terms of their ability to describe the growth of BSA in beef cattle and to detect the best estimator. Fifty-three meat cattle (20 males and 33 females) were used, mostly «Bruna dels Pirineus» and their crosses, with ages between 205 and 407 days, estimated live weight of 543±74 kg, which were slaughtered in a commercial abattoir. After the skinning, a photograph of the extended leather was obtained and using digital methods the BSA was calculated. The BSA was 3.79±1.37 m2 (range 2.55-8.12 m2). Hogan and Skouby formula appeared as the most accurate estimating formula with a determination level of over 58%, the difference in the values being due probably to the surface of the head and the distal parts of the limbs which were not considered in the study, as they were separated in the process of skinning. Among the non-linear models, the best fit was the logistic one, but with a much lower determination level of around 2%. Data shows, moreover, that, in beef cattle, body area has not reached yet its definitive development at 400 days of age. This fact should be considered when setting surface body development and new estimating formulas.
Key words: allometry; logistic model: von Bertalanffy model; Gompertz model; ontogeny
INTRODUCCIÓN
El término «función de crecimiento» suele usarse para denotar una función analítica que puede transcribirse como una única ecuación (France et al., 1996). Las funciones de crecimiento proporcionan un resumen matemático del crecimiento de un organismo o parte de él con el paso del tiempo (France et al., 1996). Así, una función general del crecimiento del área A con el tiempo t sería transcrita como A=f (t).
El uso de funciones de crecimiento es en gran parte empírica (France et al., 1996; Paine et al., 2012). Las curvas definidas por estas funciones tienen una forma de tipo sigmoideo, en la que el grado de crecimiento se incrementa a medida que el tamaño aumenta, llegando a un máximo con un punto de inflexión, y decreciendo entonces en una asíntota superior, lo que hace que recuerden la forma de «S» rotada (Birch 1999). Se pueden diferenciar en estas curvas las siguientes fases (Domínguez-Viveros et al., 2013):
1. Fase de aceleración, que se caracteriza en una velocidad de crecimiento muy rápida y positiva, llegando al máximo en el punto de inflexión; 2. Fase de desaceleración, en la que a partir del punto de inflexión la tasa de crecimiento comienza a disminuir; y 3. Fase lineal, en la que el animal deja de crecer o el crecimiento puede ser considerado como una mera reposición de tejidos. La forma y características de la curva de crecimiento pueden variar en función del ambiente y del sistema de producción (Domínguez-Viveros et al., 2013).
La mayoría de los fenómenos biológicos de crecimiento suelen encajar en los modelos no lineales, que, además, frecuentemente muestran un mejor comportamiento a la extrapolación (Payandeh, 1983). Los modelos logísticos de Gompertz y de von Bertalanffy son algunas de las funciones de crecimiento (France et al., 1996). Estos modelos presentan dos parámetros, a y c, de interpretación biológica y uno, b, definido como constante matemática. El parámetro a correspondería al área asintótica o ‘área a la madurez’. El parámetro c corresponde a la estimativa de precocidad; cuanto mayor sea el valor de este parámetro más precoz es el animal y viceversa. El parámetro b, denominado parámetro de integración, no posee significado biológico.
El establecimiento del área corporal (Body Surface Area, BSA) es necesario para estudios de adaptación climática (Daniell et al., 2012; Kasabova y Holliday, 2015), farmacológicos (Daniell et al., 2012; Jones et al., 2015; Itoh et al., 2016), metabólicos (Elting, 1926; Berman, 2003; Daniell et al., 2012), para la evaluación de quemaduras (Daniell et al., 2012) y en veterinaria forense (Henríquez et al., 2013), entre otros. El cálculo de la BSA en seres humanos se remonta al siglo XVIII, cuando Abernathy midió directamente la superficie de la cabeza, mano y pie con papel de forma triangular (Daniell et al. 2012).
La primera ecuación desarrollada para estimar la BSA fue la de Meeh en 1879 (Hogan y Skouby, 1923; Daniell et al., 2012), que incluía el peso vivo (PV), como predictor, y que estaba basada en la proposición euclideana de que para cuerpos de similar forma, el área de la superficie es proporcional a dos tercios de su volumen (Berman, 2003). En la estimación de Meeh, BSA (cm2) = K × (PV en kg)2/3, donde K es una constante de la forma, cuyo valor difiere entre especies (Jones et al., 2015); por ejemplo, 10.1 para perros y 10 para gatos (Aiello et al., 2016).
Se reconoce que los animales no son isométricos; o sea, que sus órganos generalmente no presentan un escalado lineal con el cuerpo (Howland et al., 2004). La duda que aparece, pues, es si el crecimiento de la BSA es isométrico. Si no fuese así, la utilización genérica de todos los estimadores lineales de BSA produciría estimaciones inexactas. El objetivo de este trabajo fue comparar algunas fórmulas tradicionales de estimación de la BSA y algunos modelos no lineales de peso vivo BSA como modelos de descripción del crecimiento de la BSA en bovinos de aptitud cárnica, detectar el mejor modelo y determinar su capacidad de estimación.
MATERIALES Y MÉTODOS
Se trabajó con una muestra de 53 bovinos (20 machos y 33 hembras) de diversas razas de aptitud cárnica, básicamente Bruna de los Pirineos, y sus cruces. Los animales tenían entre 205 y 407 días de edad y un peso vivo estimado de 543 ± 74 kg en el momento del sacrificio en un matadero frigorífico de la Seu d’Urgell, en Cataluña (NE España). Después del desollado, se extendió la piel y se fotografió incluyendo un patrón lineal. Posteriormente, se obtuvo el área corporal y la longitud corporal (distancia medida desde la base de la cola a la cruz) a partir de esta imagen utilizando el paquete informático Digimizer v. 4.6.1g (www.digimizer.com). En el cuero no se incluyeron las partes correspondientes a la cabeza y cola, ni las partes distales de las extremidades (la sección se hacía a nivel de carpo y tarso). La piel prepucial y de la ubre fue considerada.
Se registró el sexo, raza y edad de cada animal, así como el área de la canal caliente (±0.1 kg). El peso vivo se estimó a partir de considerar el rendimiento en un 52.5% (el rendimiento oscila entre 50 y 55% en el vacuno pesado español) (Ministerio de Medio Ambiente y Medio Rural y Marino, 2008). Al no haber diferencia estadística entre sexos (test de Mann-Whitney reflejó un valor U=235), p>0.05), se trabajó con los datos sin separación de género.
Los modelos lineales estudiados fueron los de Mitchell [0.09 × PV0.69], Brody [0.14 × PV0.57], Johnson et al. [0.235 × PV0.49], Moulton [0.158 × PV5/8] y Hogan y Skouby [PV0,4 × (longitud corporal)0.6 × 217] (Bernan, 2003), estableciendo los valores para cada animal y cada fórmula en una hoja de cálculo Excel®.
Los modelos no lineales estudiados fueron el logístico [y=a/(1+be-cx)], el de Gompertz [y=a*exp(b*exp(cx))] y el de von Bertalanffy [y=a(1-be-cx)], en los que a = estimativa del área a la madurez, b = parámetro de integración sin significado biológico, y c = estimativa de precocidad de madurez (Hammer, 2002). Cuanto mayor es el valor de c, más rápidamente el animal va a alcanzar su área adulta.
En primer lugar, se estableció la estimación de la BSA según la función alométrica y=10bxa (Reiss, 1989)(obtenidos a partir de la transformación logarítmica en base 10 de las variables, utilizando como variable independiente el peso vivo estimado), a fin de saber si el comportamiento de la BSA con el peso era isométrico o no. Un exponente a entorno de 1, indicado por una línea recta, indicaría isometría; un exponente mayor, indicaría una alometría positiva respecto del peso; es decir, con un crecimiento desproporcionadamente alto (Hammer, 2002).
Para analizar la capacidad de ajuste de cada fórmula y modelo de estimación fueron utilizados el coeficiente de correlación de Spearman r , puesto que la distribución de las BSA no era normal (reflejado por el test de Shapiro-Wilk: W=0.648, p<0.0001). Se compararon igualmente mediante un análisis de covarianza de una vía. En el caso de los modelos no lineales, se obtuvo el criterio de información de Akaike (AIC), con el planteamiento AIC=N *ln(sc/N)+(2k+1), donde, N = número de observaciones, sc = suma de cuadrados de los residuales y k = número de parámetros en el modelo (Domínguez-Viveros et al., 2013). El modelo con el valor menor se consideró como de mejor ajuste. Además de este criterio matemático para determinar cuál es la capacidad de ajuste de un modelo frente a otro, es necesario tener en cuenta como parámetro de evaluación la coherencia biológica del parámetro estimado del modelo – que depende del conocimiento que tenga el investigador del fenómeno biológico en estudio –.
Los modelos no lineales fueron ajustados al PV de cada animal utilizando el procedimiento para modelizaciones del programa PAST (Hammer et al., 2001). Este mismo paquete se utilizó para el análisis de los datos. El nivel de confianza utilizado fue del 5%.
RESULTADOS Y DISCUSIÓN
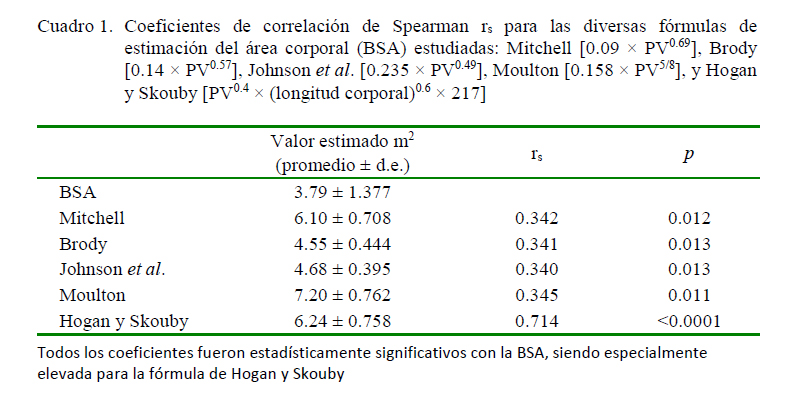
La BSA promedio fue de 3.79 ± 1.37 m2 (rango 2.55 – 8.12 m2). Los coeficientes correlación de Spearman rs para las diversas fórmulas de estimación de la BSA aparecen en el Cuadro 1 y los valores AIC de los modelos no lineales en el Cuadro 2. Todos los coeficientes en las fórmulas de estimación estuvieron significativamente correlacionados con la BSA real, siendo la de Hogan y Skouby la que presentó el mejor valor (r =0.714, p<0.001). El análisis de covarianza no reflejó diferencias entre los valores del presente estudio y los estimados por la fórmula de esos autores (F=2.176, p=0.143) (Figura 1).
La fórmula de Hogan y Skouby parecería ser la más ajustada de las cuatro fórmulas consideradas, con un coeficiente de determinación R2 de 0.585, siendo la diferencia en los valores la ausencia de la superficie de la cabeza y de las partes distales de las extremidades, que no fueron consideradas en este trabajo. La función alométrica quedaría establecida como BSA (m2) = 100.452 × PV (kg)1.549, indicando claramente una alometría positiva, no isométrica (Figura 2).
Entre los modelos no lineales, el menor valor de AIC (111.02) fue observado para el modelo logístico (Figura 3). Este modelo, en lugar de estimar los valores reales de la variable de interés, como el anterior, se construye una función basada en el cálculo de la probabilidad de que la variable de interés adopte el valor del evento previamente definido. Para los datos aquí considerados, el modelo logístico tendía a subestimar el área inicial. Apareció una correlación estadísticamente significativa entre los valores estimados por esta función y la BSA real (r =0.340, p=0.01), aunque con un bajo nivel de determinación, R2=0.029. Cabe decir, además, que aunque los registros de pesaje de estos animales se llevaron hasta los 584 kg de peso vivo estimado y los 407 días de edad, fue imposible establecer con claridad la fase asintótica de la curva en el modelo logístico. La estimativa del área final (parámetro a) fue el mismo para todos los modelos. Las tasas de madurez (parámetro c) para los tres modelos aparecieron igualmente similares.
No alcanzar el punto asintótico en el modelo no lineal logístico, su bajo coeficiente de determinación, así como el comportamiento lineal claramente no isométrico, indica que aún no se ha llegado a la superficie corporal definitiva a los 400 días de edad en bovinos de engorde. Es lógico pensar si a esa edad el bovino aún no ha llegado a su desarrollo completo (Marinho et al. 2013), su BSA tampoco lo ha hecho, bajo el postulado de que si la similitud geométrica se mantiene con el incremento del tamaño, o sea con la edad, exhibirán una ratio área/volumen continuamente decreciente (Gould, 1966). Este hecho debería tenerse en cuenta al establecer curvas de desarrollo corporal y fórmulas estimativas más ajustadas.
CONCLUSIÓN
En bovinos de engorde, el área corporal no ha llegado aún a su desarrollo definitivo a los 400 días de edad.
Agradecimientos
El autor agradece el matadero frigorífico MAFRISEU SA por haber permitido el acceso a los animales, así como a toda la información asociada. Miquel Àngel Albertón, veterinario responsable del establecimiento, ofreció igualmente en todo momento su máxima colaboración.
Literatura citada
1. Aiello SE, Moses MA, Allen DG. 2016. The Merck Veterinary Manual. 10th ed. Kenilworth, NJ/ : Merck & Co.
2. Berman A. 2003. Effects of body surface area estimates on predicted energy requirements and heat stress. J Dairy Sci 86: 3605-3610. doi: 10.3168/jds.S0022-0302(03)73966-6
3. Birch CPD. 1999. A new generalized logistic sigmoid growth equation compared with the Richards growth equation. Ann Bot-London 83: 713-723. doi: 10.1006/anbo.1999.0877
4. Daniell N, Olds T, Tomkinson G. 2012. Technical note: criterion validity of whole body surface area equations: a comparison using 3D laser scanning. Am J Phys Anthropol 148: 148-155. doi: 10.1002/ajpa.22051
5. Domínguez-Viveros J, RodríguezAlmeida A, Núñez-Domínguez R, Ramírez-Valverde R, Ortega-Gutiérrez JA, Ruiz-Flores A. 2013. Ajuste de modelos no lineales y estimación de parámetros de crecimiento en bovinos tropicarne. Agrociencia 47: 25-34.
6. Elting EC. 1926. A formula for estimating surface area of dairy cattle. J Agric Res 33: 269-280.
7. France J, Dijkstra J, Dhanoa M. 1996. Growth functions and their application in animal science. Ann Zootech 45(Suppl 1): 165-174. doi: 10.1051/animres:19960637
8. Gould SJ. 1966. Allometry and size in ontogeny and phylogeny. Biol Rev 41: 587-638.
9. Hammer Ø. 2002. Morphometrics. Brief notes. Zurich. [Internet] Available in: http://folk.uio.no/ohammer/past/ morphometry.pdf
10. Hammer Ø, Harper DAT, Ryan P D. 2001. PAST v. 2.17c. Palaeontol Electron 4: 1-229.
11. Henríquez AL, Landaeta-Aqueveque C, Larenas J. 2013. Cinética del algor mortis. Primeros pasos para estimar data de muerte en animales. Arch Med Vet 45: 77-81. doi: 10.4067/S0301-732X2013-000100013
12. Hogan AG, Skouby CI. 1923. Determination of the surface area of cattle and swine. J Agric Res 25: 419-432.
13. Howland HC, Merola S, Basarab JR. 2004. The allometry and scaling of the size of vertebrate eyes. Vision Res 44: 2043-2065. doi: 10.1016/j.visres.2004.03.023
14. Itoh T, Kawabe M, Nagase T, Endo K, Miyoshi M, Miyahara K. 2016. Body surface area measurement in laboratory miniature pigs using a computed tomography scanner. J Toxicol Sci 41: 637-644. doi: 10.2131/jts.41.637
15. Jones KL, Granger LA, Kearney MT, da Cunha AF, Cutler DC, Shapiro ME, Tully TN, et al. 2015. Evaluation of a ferret-specific formula for determining body surface area to improve chemo-therapeutic dosing. Am J Vet Res 76: 142-148. doi: 10.2460/ajvr.76.2.142
16. Kasabova BE, Holliday TW. 2015. New model for estimating the relationship between surface area and volume in the human body using skeletal remains. Am J Phys Anthropol 156: 614-624. doi: 10.1002/ajpa.22678
17. Marinho K, Freitas A, Falcão A, Dias F. 2013. Nonlinear models for fitting growth curves of Nellore cows reared in the Amazon Biome. Rev Bras Zootecn 42: 645-650. doi: 10.1590/S1516-35982013000900006
18. Ministerio de Medio Ambiente y Medio Rural y Marino. 2008. La clasificación de canales de vacuno pesado. Base legislativa y manual gráfico. Madrid, España: Ministerio de Medio Ambiente y Medio Rural y Marino. 53 p.
19. Paine CET, Marthews TR, Vogt DR, Purves D, Rees M, Lindsay AH. Turnbull Paine. 2012. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol Evol 3: 245-256. doi: 10.1111/j.2041-210X.2011.00155.x
20. Payandeh B. 1983. Some applications of nonlinear regression models in forestry research. Forest Chron 59: 244- 248. doi: 10.5558/tfc59244-5
21. Reiss MJ. 1989. The allometry of growth and reproduction. Cambridge, UK: Cambridge University Press. 182 p.
Recibido: 20 de marzo de 2018
Aceptado para publicación: 31 de agosto de 2018