Local well-posedness for a Cauchy problem associated to a non linear evolution equation
DOI:
https://doi.org/10.15381/pesquimat.v24i2.21697Keywords:
non linear KdV-Kuramoto-Sivashinsky equation, periodic Sobolev spaces, local well posedness, Semigroups theory, Fourier theory, Banach's fixed point theoremAbstract
In this article we will study the local well-posedness for a non-linear Cauchy problem associated with the differential equation KdV- Kuramoto-Sivashinsky:
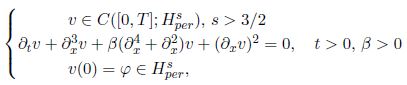
in the infinite dimensional spaces (periodic sobolev) H sper. We do this using the theory of C0- semigrupos, main properties of the Fourier transform in H sper, as the inmersions in these spaces and that H s-1per is a Banach algebra, which allows us to justify the presence of the non-linearity 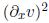 .
.
Downloads
Published
Issue
Section
License
Copyright (c) 2021 Luis Milla Garcia, Yolanda Santiago Ayala

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
THE AUTHORS RETAIN THEIR RIGHTS:
a) The authors retain their trademark and patent rights, and also on any process or procedure described in the article.
b) The authors retain the right to share, copy, distribute, execute and publicly communicate the article published in Pesquimat magazine (for example, place it in an institutional repository or publish it in a book), with recognition of its initial publication in the Pesquimat magazine.
c) The authors retain the right to make a later publication of their work, to use the article or any part of it (for example: a compilation of their works, notes for conferences, thesis, or for a book), provided that they indicate the source of publication (authors of the work, magazine, volume, number and date).






